Euler equations

From practical experience we know that the solution $f(\theta)$, which describes the movement of a harmonic oscillator, behaves as a real sinusoidal function. So the question is how the general complex exponential solution, as introduced here, relates to the expected real sinusoidal solution. In order to show this first the Taylor series is introduced.

Taylor expansion

Every function can be approximated by a polynomial function. This approximation is also known as a Taylor series or Taylor expansion. The Taylor expansion of any differentiable function $f(x)$ in the point $x=\alpha$ is given as $$ f(x) \approx f(\alpha) + \frac{f^\prime(\alpha)}{1!}(x-\alpha) + \frac{f^″(\alpha)}{2!}(x-\alpha)^2 + \frac{f^‴(\alpha)}{3!}(x-\alpha)^3 + \dots$$ where $n!$ denotes the factorial of $n$ is calculated as $n\cdot(n-1)\cdot\ldots\cdot 2\cdot 1 $, so as an example $3! = 3\cdot 2\cdot 1 = 6$ and $f^{(n)}(x)$ is the $n^{th}$ derivative of the function $f(x)$.

When $\alpha = 0$ the approximation simplifies to $$ f(x) \approx f(0) + \frac{f^\prime(0)}{1!}x + \frac{f^″(0)}{2!}x^2 + \frac{f^‴(0)}{3!}x^3 + \ldots = \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n,$$ which is also known as the Maclaurin series. This series can be calculated for all functions. The series of several frequently used functions are

$$ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!}\ldots,$$

$$ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \ldots$$ and $$ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \ldots.$$

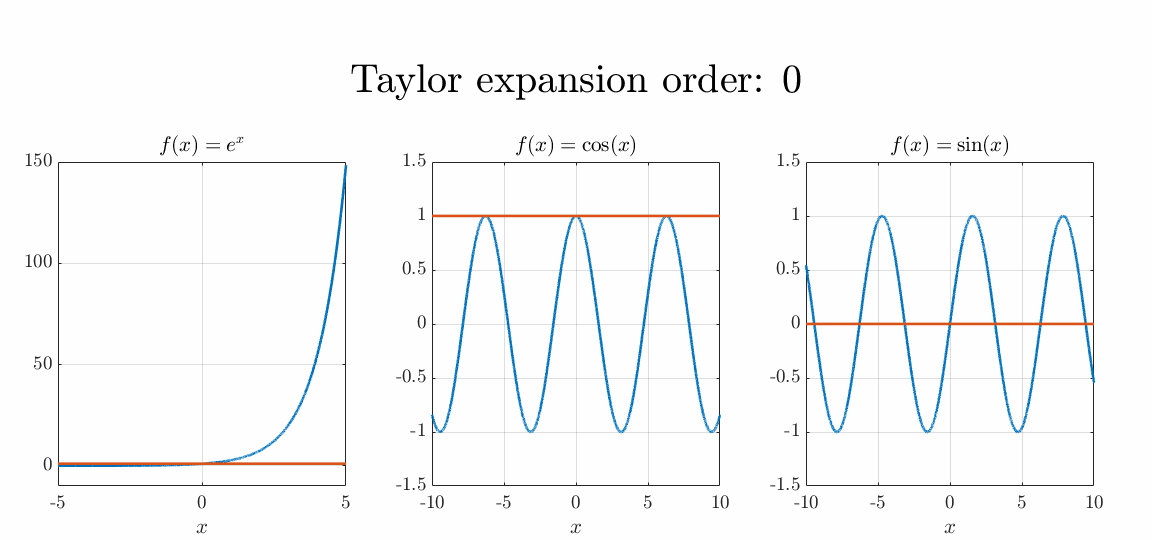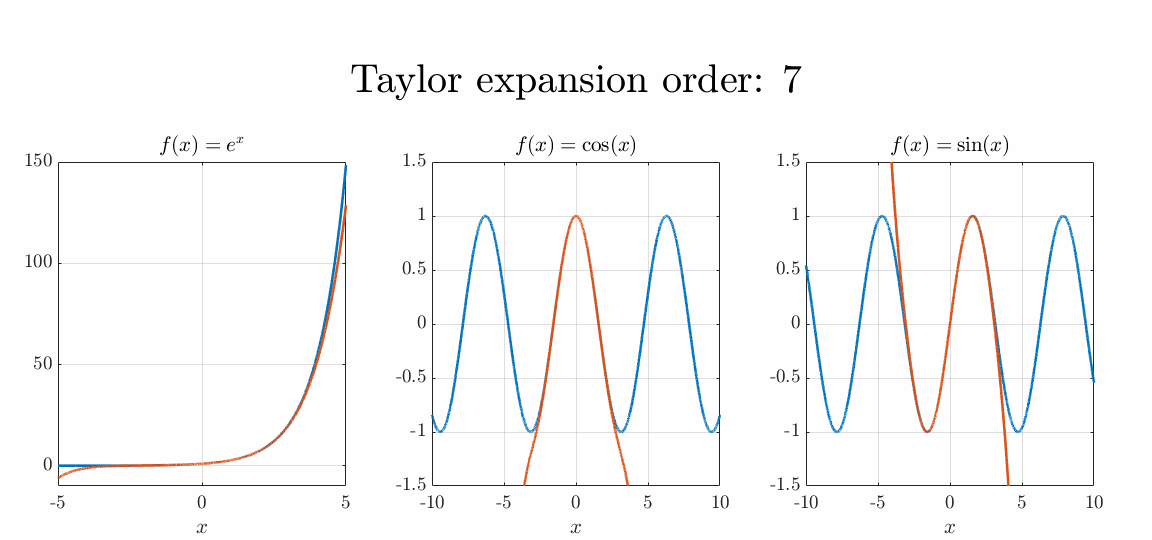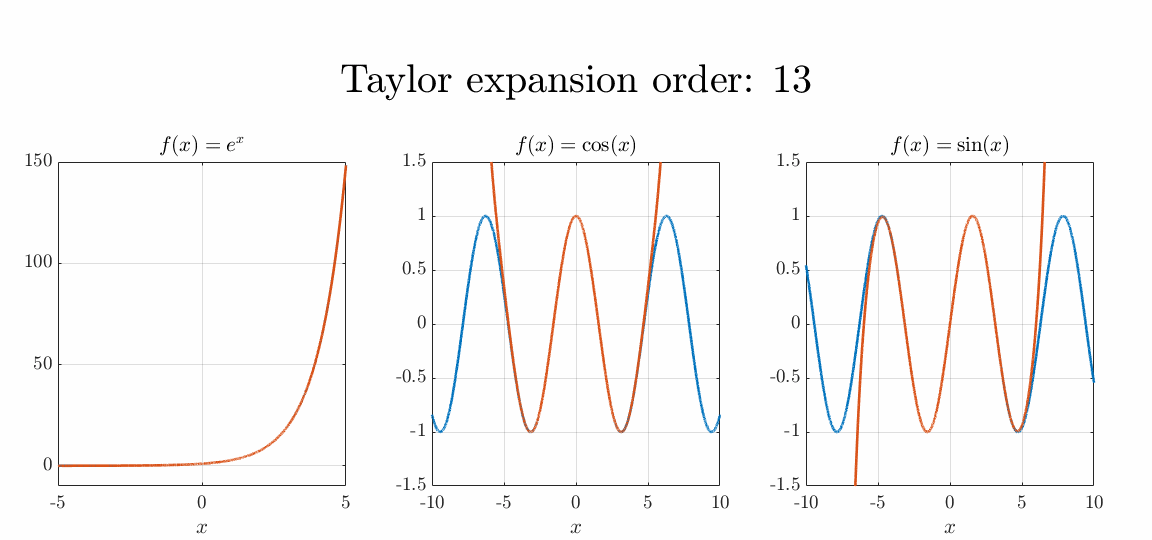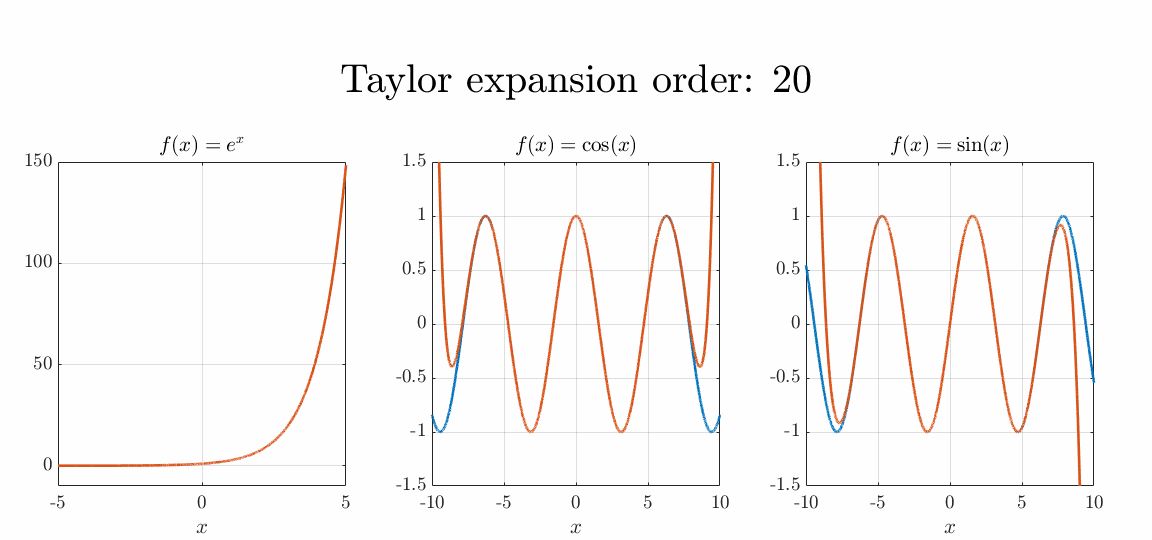
Euler equations

When returning to the example of the harmonic oscillator we found that the solution was given as $f(\theta) = e^{j\theta}$. This function is often called a complex exponential, since a complex number is the exponent. In order to show the link between this function and a sinusoidal function, as is observed in practice, the Maclaurin series of this function needs to be determined as $$ e^{j\theta} = 1 + j\theta + \frac{(j\theta)^2}{2!}+ \frac{(j\theta)^3}{3!}+ \frac{(j\theta)^4}{4!}+ \frac{(j\theta)^5}{5!} + \ldots.$$ This equation can be simplified by using the definition of the complex unit $j=\sqrt{-1}$, which can be used in determining the following terms: $$ j^2 = -1, \qquad j^3 = -j, \qquad j^4 = 1, \qquad j^5 = j$$ Rewriting the Maclaurin expansion now gives us $$ e^{j\theta} = 1 + j\theta - \frac{\theta^2}{2!}-j \frac{\theta^3}{3!}+ \frac{\theta^4}{4!}+ j\frac{\theta^5}{5!} + \ldots.$$ Upon closer inspection this representation allows us to split the expression in a real and imaginary part as $$ e^{j\theta} = \left(1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \ldots\right)+ j\left(\theta - \frac{\theta^3}{3!}+ j\frac{\theta^5}{5!}-\ldots\right).$$ Now recall the Maclaurin series of the sine and cosine function and substitution will give rise to the Euler equation $$ \bbox[5px,border:1px solid black]{e^{j\theta} = \cos(\theta) + j\cdot\sin(\theta)} $$

Representation of sin(x) and cos(x)

Now we can use the Euler equation to find alternative expressions for the sine and cosine functions. For this we first evaluate the Euler equation for $-\theta$, which results in $$ e^{-j\theta} = \cos(-\theta) + j\cdot\sin(-\theta) = \cos(\theta) - j\cdot\sin(\theta).$$ Now by adding or subtracting this equation to the Euler equation we obtain the following two equations: $$ e^{j\theta} + e^{-j\theta} = (\cos(\theta) + j\cdot \sin(\theta)) + (\cos(\theta) - j\cdot \sin(\theta)) = 2\cos(\theta)$$ $$ e^{j\theta} - e^{-j\theta} = (\cos(\theta) + j\cdot \sin(\theta)) - (\cos(\theta) - j\cdot \sin(\theta)) = 2j\sin(\theta)$$

From this we obtain the following alternative expressions for the sine and cosine functions as sums of complex exponentials: $$ \bbox[5px,border:1px solid black]{\cos(\theta) = \frac{e^{j\theta}+e^{-j\theta}}{2}} \qquad \bbox[5px,border:1px solid black]{\sin(\theta) = \frac{e^{j\theta}-e^{-j\theta}}{2j}} $$

As is the case with differential equations, all linear combinations of the complex exponential are also valid solutions of the second order differential equation of the harmonic oscillator. As a result it follows from the alternative representations of the sine and cosine function that the sinusoidal functions are the real solutions of the second order differential equation and we can generalize these real solutions to a complex exponential solution.